Quite recently I've recieved a book back to my hands from the year 2011, the book is called «Algorithms in C++», authored by Robert Sedgewick. It returned after a long wait on a bookshelf in my parents' home. My young mind of a first-grade bachelor student could not understand such a rich material back then, and there was a lot of study courses after all. But I wanted to buy it so badly, so there it is now, had to wait quite a lot...

This book is definately wonderful, although seems to be not so popular as Cormen textbook. As far as I understand, now Sedgewick course is more popular without C++ context, in general, but personally I love C++. This is how it looks like, I have one with almost the same cover:

First chapter here is a gentle introduction which aims to get the attention of everyone with even slight interest to algorithms, and the task under consideration is so called dynamic connectivity problem (DCP).

Here is the main point of the problem: Input consists of pairs of integers (more precisely - non-negative integers), let's call each one (p,q). Each number in pair represents some vertex in graph, and a pair itself is an edge in a graph between vertices called p and q. Edges provide connections in graph, and connectivity relation (i.e. the fact that two vertices are connected with edge) has the following properties:

• it is symmetric (if p is connected to q, then q is connected to p),

• it is transitive (if p is connected to q and q is connected to m, then p is connected to m).

If we would also add that any p is connected to itself, such a relation would be called an order in mathematical sense.

Output of the program should be only the pairs, that could not be derived using connectivity properties from the previous pairs of input.

For better understanding consider the following example:

Input: (1,2), (1,3), (2,4), (4,3), (5,2), (5,4)

Output: (1,2), (1,3), (2,4), (5,2)

In other words, this program has to dynamically drop all the redundant edges from input and return only edges from spanning tree.

The first proposed algorithm (which is, of course, not optimal) is a so called fast search method. The idea of the method is quite simple, yet beautiful: let us think of any vertex as a container with mark, and this mark is an ID of some vertex in graph (initially every vertex has it's own ID as a mark). After we see some pair of vertices IDs as an input, we have to check marks on this vertices, and if their marks are different we have to change marks of all known vertices in graph, so that they can store information about this new connection (i.e. all vertices in one connected component are marked with the same ID). This way mark of any vertex will be in fact an ID of a connected component in graph.

I will go against Sedgewick's will in this book and write some example code here in Python, not in C++. Let's assume that inputs are recieved via text file, each new input pair is written in next line and elements in every pair are separated with space. Output will be printed out in console in the same format as input. The following code has demo-only purpose and may appear as a quite messy one to some readers:

Ok, now before we move on, let's think a bit why this method is good, and in what way it can be better?

First thing to see is that in case when new pair that comes as input is a redundant one, then we will get rid of this pair instantly — that is just the thing we do in lines 10 and 11. It is quite cool, but we pay great price for such speed — we have to go through all the dictionary called ids to be able to search so quickly (that is done in lines 13-15).

Being extremely boring we can say that algorithm can be divided in two parts — union and find. Find is a part of checking that input pair is redundant or not, and union is a part where we make some work to keep actual indexing of connected components. In this terms the proposed fast search method makes no more than MxN operations to solve DCP when there are N objects, for which M union operations are required. This is a simple statement to prove and I would suggest you to prove it yourself (or refer to the textbook that I mentioned if proof will be to hard to deduce).

In that case one should be craving to speed up union operation paying with some speed of find operation as a price. Let us try to do that by changing different types of marks for each vertex. We shall store «delegate» for each vertex, and make it in such a way that the most valuable «delegate» will always appear at the end of a list of delegates. Let us call such an approach a fast union method and take a look at example code:

Now union operation does not require traversing all of the elements in ids dictionary, we only have to run through a list of delegates for each vertex in input pair — this looks cheaper than previous approach (and in average it actually is), but it is easy to see that there are terrible cases of inefficient behavior of this method (please, take a minute and think about a «bad» input pairs sequence, i.e. such a sequence when the quick union algorithm will work slowly).

Sure thing you will quickly find the «root of evil» of this approach — if you think of information about delegates as a tree (i.e. have an edge from each vertex to its delegate after processing each input pair) then some of the recieved trees will be quite unbalanced (and it is a cause of major slowdown in some cases). In that case we can easily come up with a solution — let's perform our own tree-balancing, i.e. by weight of a subtree, where weight will be number of vertices in a subtree. But it is better to see the code once, than describe it a thousand times, so I invite you to look at an example code and call this a weighted fast union method:

Well, now it is clear, such a method will try to pick lighter subtrees and connect them to the heavier ones, and this will guarantee some tree balancing! I propose a bit more difficult mathematical statement for you to prove by yourself as an exercise (here we have a base two logarithm):

During a weighted fast union method work, to find that two input vertices are connected we need to follow no more then log(N) pointers, in case we have N vertices in total.

This statement will be true due to the fact, that union operation preserves estimate of a height from the root to the end-node in a list of delegates in every step of the algorithm. If you cannot fight this proof by your own, please refer to Sedgewick's wonderful textbook.

Well, this already seems quite optimal, what can become better? In fact a lot of things. In the textbook some modifications are presented which base on the shortening of paths inside delegates tree, which amortize processing time for each search queries while paying the small price of tree-restruct. These modifications are very curious and you can definately derive some of them by your own — try to think if we can get rid of long paths in the delegates tree if at the end of the day we are only interested in the final node inside the path? What will it cost to keep a tree not only balanced but purely flat?

To clarify things I tried to visualize a delegates tree for all three methods presented in the text above, when the input sequence is the following: (1,2), (2,3), (4,5), (5,6), (3,4), (6,7), (7,8):

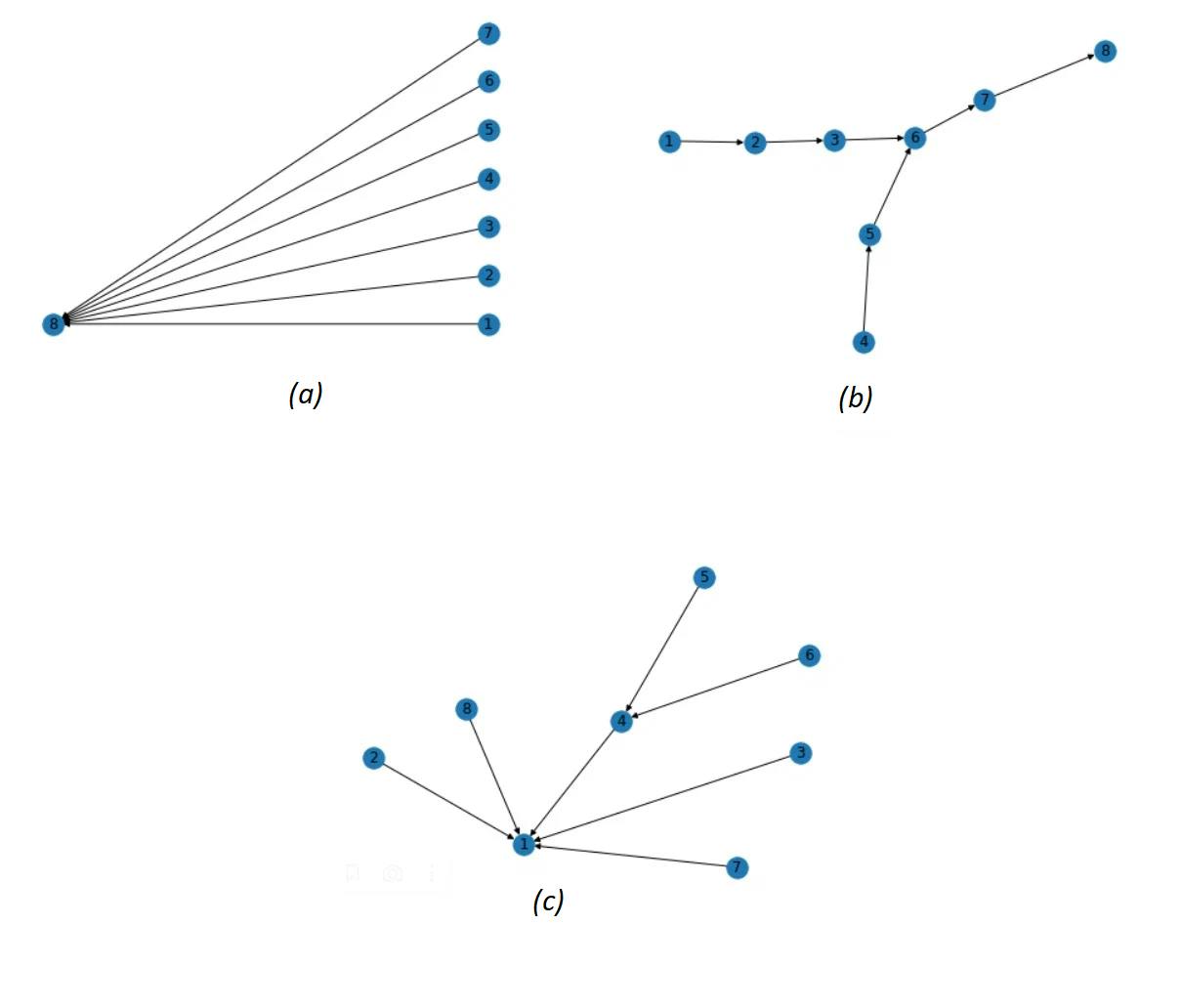
Here in (a) we see the tree for quick find method (and it is perfectly flat), in (b) it is a tree for quick union method (and it is a lot worse in terms of three height), and in (c) it is a tree for weighted fast union method (this one is a lot better than (b)).

In fact, I found particular interest for DCP task after reading some exercises from chapter 1 of the textbook, one of which seems to be quite useful for better understanding of weighted fast union method. Here is the exercise:

Find an average path length from root to the end node in the worst case of a 2^n vertex tree, built using weighted fast union method.

If you read this exercise not very carefully (as I did, for sure) at a first glance you can think that the task was already solved here in the text above, but the main word in exercise formulation is average. We already know maximum length - it is not more than n if we have 2^n vertices, this is derived from the exercise mentioned earlier.

This task only looks scary, as a matter of fact it is not so hard. Try to solve it by yourself first, but I will put here some insights for the solution and the answer that I've got.

In the worst case we always make union of subtrees of the same weight, that is when we build the longest path. Consider case of n=3 and the following input sequence: (1,2), (3,4), (5,6), (7,8), (1,3), (5,7), (1,5). You can try to visualize this sequences using several rounds of tree-building. On the first round we build 4 paths of length 1 (after input pair (7,8)), i.e. half of the vertices will have zero height and the other half height will increase by 1. After that on the second round we form two subtrees, each of which has a sequence of length 2 (after pair (5,7)). These two subtrees are formed by concatenation of pairs of sequences of length 1, and we have just the same process: half of vertices increase their height by 1, other half remains on the same height. Last round builds a path of length 3, after input pair (1, 5). Here we again see half of vertices that do not change height, and the other half increased height by 1. We have n rounds (since it was log(2^n)), each round sum of lengths of sequences is increase by 0.5 (2^n) = 2^(n-1). Initial length was obviously zero, so average will be: (n2^(n-1))/(2^n) = n/2.

In this sketch of a proof I do not explain why it is actually the worst case. This is made intentionally, so that you can think of it by yourself. Or maybe you can find some flaws in my proof and write your own in the comment section, feel free to do that!

Thank you for reading, please subscribe for new articles!

Wish you good luck and perfect balance (just like the balanced trees have, or even better)!