What I actually like to do is to describe some algorithms from the most naive approach to quite complicated ones. It is also very satisfying when there are both complex and simple algorithms that improve a lot compared to naive ones, and one can see the beauty of all of them. This is exactly what you can find when start studying a substring search task in most of the courses on algorithms. Let's try to dive a bit into this topic today, here is the task we'll be solving:
Given two strings (sequences of characters in some finite alphabets, usually called needle and haystack) with lengths n and m (n < m) it is required to find all the appearances of the shorter string (needle) inside the longer one (haystack). By appearance, we mean that inside the longer string, there may be a subsequence of symbols going one by one which exactly repeats the shorter string.
Ok so for example inside a string 'abcdef' we can find the appearance of substring 'cd' on position 2 (start indexing from 0), but we don't have any appearance of substring 'cc', for example. We need to design an algorithm to find all appearances and one can easily give a naive approach which is just 'search through and compare all the symbols one by one', like this:
It's quite easy to see the problem with this algorithm: although it does not require any additional memory, running time will be O(n*m) in the worst case, since in the worst case for any symbol of haystack we will need to make m comparisons until the break condition on line 10 is true. Let's look at the example of worst-case test:
It took 94 seconds for 50 runs on this test, and it is obvious that for such needle and haystack, our break condition on line 10 of the naive algorithm code snippet will be true only at the end of the substring that we try to compare, which is why time complexity is so bad. Can we do better? Certainly, we can and I would like to tell you two different approaches to how to do it.
There is a family of algorithms that are based on the idea of prefix-function and z-function which can achieve good time complexity. I will outline only one of them, but you can find out a lot more. Here we'll be talking about a z-algorithm which is based on the idea of z-function. What is z-function anyway?
In simple words, z-function for a given string is just an array of numbers with the length equal to the length of the string, where each number on position i is equal to the length of the prefix, which is equal to substring starting from position i. Sounds complicated, but actually, it is quite simple. Look at the example (taken from here, actually):
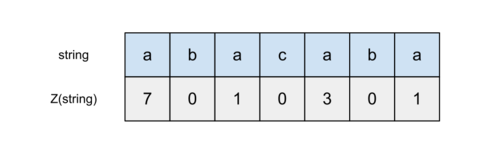
The first line here is the string of characters, second is the calculated z-function. The first element in the array of z-values may be the length of the entire string or zero, it actually does not matter. What really matters are the other values, for example on position 2 (indexing from 0) we have z-value equal to 1, since the largest substring equal to the prefix from this position is just the letter 'a'. For position 4 z-value is 3 because the prefix 'aba' is exactly the same as the substring of length 3 starting from position 4. So now the concept of z-function must be a bit more clear to you. But why do we need it?
Using z-function we can ease up finding all substrings inside text. Suppose we somehow calculated z-function for the following string: needle + '$' + haystack, where '$' is just some symbol that does not appear in the needle on haystack strings. Then we can just look through the array of z-values, and find out all the positions where z-value is equal to the length of the needle, which will mean that this position is a start of a substring equal to the prefix length equal to the length of the needle. This will require O(m) time only. Neat, right? But how can the z-function be effectively found and what is the time complexity of this calculation? Here I would prefer to show the code first, and then tell a couple of words. Take a look:
Let's think a bit about how we calculate z-values. We suppose 'i' is a current position, 'left','right' - some borders of known prefixes. On line 5 we init a z-value with max(0, min(right-i, result[i-left])). Right-i could be negative if right < i - then initialized with 0. Otherwise, we have put the right pointer ahead of i, which means we already looked forward in the array until the right pointer. The left pointer will always be less than i (except for the first step), so result[i-left] always points either to z-value to the left of i, which should be already calculated for i>0. So the 'right' pointer is our 'horizon' and 'left' pointer is memory. On lines 6,7 we try to look ahead from the horizon and increase z-value if possible, and on lines 8,9,10 we update the pointer. I think that is quite beautiful. But what is the time complexity? If you think a bit about this function you will notice that each position in the result array is accessed no more than two times inside z-function calculation: once it can be when i is inside [left, right], second time by the 'while' cycle. So this procedure has time complexity O(n), where n is the length of the input string. Obviously, z-function search is also linear, since we just run through the result array. Thus total complexity is O(n+m), and since m>n it actually O(m) for substring search using z-function. Let's test it:
Nice, 1.3 seconds vs. 94 in naive approach in python implementation, this is quite good. But we had to sacrifice our memory because z-function approach required us to make an array of the same size as haystack + needle. Can we do better? As they say 'if the problem seems hard to solve, try hashing'... Why don't we try it too? Take a look at the following algorithm which is called after Richard M. Karp and Michael O. Rabin:
The main idea here is using a simple hash that can be easily recomputed. We first calculate hash of the needle and then start traversing the haystack and calculating the hash of the sliding window. Hash recalc is very fast - just a few operations, see line 30. If hash function is good enough, we will usually not fall into a lot of false alarms. If hashes of sliding window and needle are equal we will check if actually we found a substring inside haystack. Very simple yet powerful.
And even though in some cases this approach can work not so well, in average its complexity shows to be also linear, without any additional memory. Let's consider just the same worst-case as we did before:
This seems to be even better than for z-algorithm in python implementation, great!
Now we have several algorithms to search a substring, but we can find much more, of course. This is a very interesting topic to study if you are learning computer science.
Of course, if you will call the simple 'find()' function in python it will work much much faster, due to more powerful algorithms and implementation in a lower-level programming language, but now you probably have some idea of what can be under the hood of fast search functions that you use.
Thank you for reading, feel free to like and comment if you enjoyed it!
Wish you all the best finding in life!

