From time to time I refer to materials of computer science courses and academic literature on math and algorithms due to large interest to the manner of how some study material can be presented to the audience. There are a lot of wonderful computer science courses out there that can serve as an inspiration for some reasearch topics for students. It requres a lot of work and skills to present some new concept smoothly so that listeners can get your ideas for real. I love task-oriented approach, when some new concept is presented through a particular problem that is solved iteratively, from the simpliest solution to the most intelligent one. In this article I would like to make a breif review of an indroductory task from the brilliant MIT 6.006(intoduction to algorithms). The problem is called a peak-finding task, and as it soon will be clear, peaks that we'll be searching for are motivated from the most natural analogy:
In the above image there are two peaks and they are found quite easily, but, of course, we'll be dealing with some numbers, where things go a bit more tough. Let us consider 1-dimensional and 2-dimensional tasks. They are very similar, in fact, and the main task is to find in 1-D or 2-D array of integer numbers any peak, where peak is a position in the input array (indexed with 1 or 2 coordinates, based on dimensionality of the task) where value in the array is a local maximum (i.e. it is not less than it's neighbours). In the 1-D task neighbours reside to the left and to the right of a given position (except for corner cases, where only one neighbour exist), and in 2-D task we search for neighbours in 4 directions: top, bottom, left, right.
To make things more clear I made a small example of 2-D array of size 10x10 filled with random numbers from -100 to 100 and selected several peaks from this array with green color (be careful, not all the peaks, just some of them):
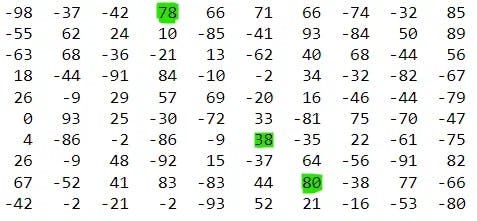
Please note that maximums are not strict — thus if we would have an array of the identical elements, they would all be considered as peak values. I think this is a wonderful choice for an introduction task, since it is so fantastically easy to be explaned to students and allows to quickly comprehend why algorithm complexity really matters. One can even find some practical use of such a task — for example if we would like to crate some engine that makes decisions quickly based on some statistical data (one can think of numbers in the array as of some costs of move, and we are intersted in any locally-optimal move).
Let's start with 1-D case. Suppose we have an n-element array of integers as an input and we have to find any local maximum (a.k.a. peak). The first and probably the most naive approach would be run through this array and stop if we found a local maximum. It is quite easy to understand that this approach requires O(n) time in the worst case (think of the worst case, make this mental excercise, before reading ahead). Below you can see a listing of such a solution and several tests (one of which is in fact a worse-case scenario for the algorithm), time is presented in seconds:
So, the worst case is when we need to traverse all the array to find a peak — it is possible if we are not lucky enough.
The good news is that we do not need to perform linear search in this task, «divide and conquer» approach can help us out. We can perform a very easy optimization called binary search: every step we will divide the task in two smaller subtasks, and will search for any peak in a smaller-sized task. When we'll select item to divide task in two smaller parts, we will first check whether the selected element is a peak already, and if it is we won't even need to search anymore. If not, we'll be moving towards the growth-direction, i.e. to the direction of the larger neighbour. Since the input array has finite size, there cannot be infinite growth of any value in any direction, thus any growth direction eventually leads us to some peak value. Here is the example listing for binary-search peak-finding solution:
Execution time for worst case got much better, and this is quite natural, since we now always divide the task in two, and time complexity becomes O(log(n)) (log is taken base 2). Try to find out why this is true for time complexity as a small exercise. The natural question though is the following: can we make even better and solve the task faster than logarithm in worst case, if we do not have any special information or restrictions on input and no specific data structure (i.e. we use arrays only)? Think about it and write your thoughts in the comment section.
Now let's move to the 2-D case, it must be more interesting, isn't it? Suppose we have an n times m integer array as an input and we have to find any peak (neighbours can be only 4 cells, top, bottom, left, right). Seems quite similar to 1-D case, but now we just have more direction to go to. Let's first try the same greedy strategy, i.e. let's always move to the direction of the largest growth of a neighbour value. Obviously this way we will eventually come to some peak (since the task has finite dimensionality), but in the worst case it can take too long if we start badly (time complexity will be O(nm)). To better understand why this is true take a look at this example, where yellow is our start point, and green is the peak value, where we are heading with a greedy approach:
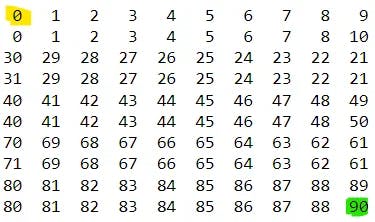
And here is the listing with this worst-case, since we all know that talk is cheap:
One can argue that I just selected the bad initial position — why should we start from top left corner? Well, as another one exercise I propose you to prove that similar time complexity worst-case example (O(nm)) can be presented for any start point that you would select. If n=m it is a quadratic complexity.
Well then, can binary search save the day? What if this method is a wonderful solution to any problem arising? In fact, it is not, but in this particular task it really can be useful. However comparing to 1-D case we now have at least two possibilities: to divide the task by rows or by columns. And where then to go after task division?
Suppose we decided to divide by rows and selected a middle row during our divide and conquer. What should we do with it then? Well, let's try to find maximum value from this row and check it for peak-property. If it is a peak, we got what we wanted. If not — move to the direction of the largest growth. Please consider thinking a bit about why we select maximum in a row, and not just any other element. Also try to think of why this algorithm will converge to the peak. All these questions seem to be intuitively clear, but in fact, they are not. Try, for example, thinking what would happen if we take not a maximum value in a row, but a peak value in a row (spoiler: everythink will break and you will be able to find an example when you then will come not to a peak, but to some dead-end). Meanwhile, the code example for such an approach is below:
Now time is much better than in linear-search greedy approach, in fact it is O(mlog(n)), or, in case of n=m it is O(nlogn). Try to prove that, but if it appears too tough for you, refer to the course materials.
The best thing I've kept to the last. Another natural question is, can we do even better than such a binary search (by rows or columns)? Can we achieve time complexity O(n) in case of matrix with n=m? In fact, yes! Authors of the mentioned course put this as an excersice to their course materials, and not many students really get to them, unfortunately. I wouldn't like to give the full solution here, since this is a brilliant exercise, but I will outline some hints for you, so that you can solve it by your own:
To get the best complexity we need to alternate rows and columns when we perform division of the task in two smaller parts. We first select the middle row, if search is not over we have to make the same with columns, and so on. This way we will localize peak value from two sides. But it is not so easy to just add new dimension for task-division process - make an example when simple alternation of rows and columns with selecting maximum value and growth direction will lead you to dead-end value, not the peak one. To solve this issue we will have to use some additional memory, i.e. we will have to remember the previous largest-growth direction cell, and compare the current largest growth with the previous one. In case if the new largest-growth direction gives less gain than previously remembered, we will have to select the opposite half of the task, to the one that we are considering now as a largest-growth subtask. Try to come up with some example matrices to get this trick right, this is not a one-second clear concept.
That's all for today's article, thank you for reading! Don't forget to subsribe and give some reactions!
Wish you all the best, stay tuned for new beautiful algorithms and always strive to the top peaks in your life! =)