Frankly, I am not very good at probability theory (yeah, I did not learn as well as I should have been). But this science is so deep and beautiful and helps in a lot of tasks (algorithmic tasks too!) that couldn't have been solved otherwise, it is worth studying. In this article, I would like to speak a bit about random choice in some logical tasks and how they sometimes can seem like the only option but be bad. As an example, I will use several well-known logical tasks and outline the ideas via python, as usual. The ideas for this topic were partially provided by my friend, who insisted to be incognito (thank you D.P.S.)!

So, if you are good in probability, you will hardly find something new today, I guess... But if not, let's peek behind the veil of randomness! (And here comes the spoiler picture)

As some of you have probably already understood, the first plot we'll be talking about is a famous Monty Hall problem. If you somehow did not hear anything about it, let me describe the problem shortly:

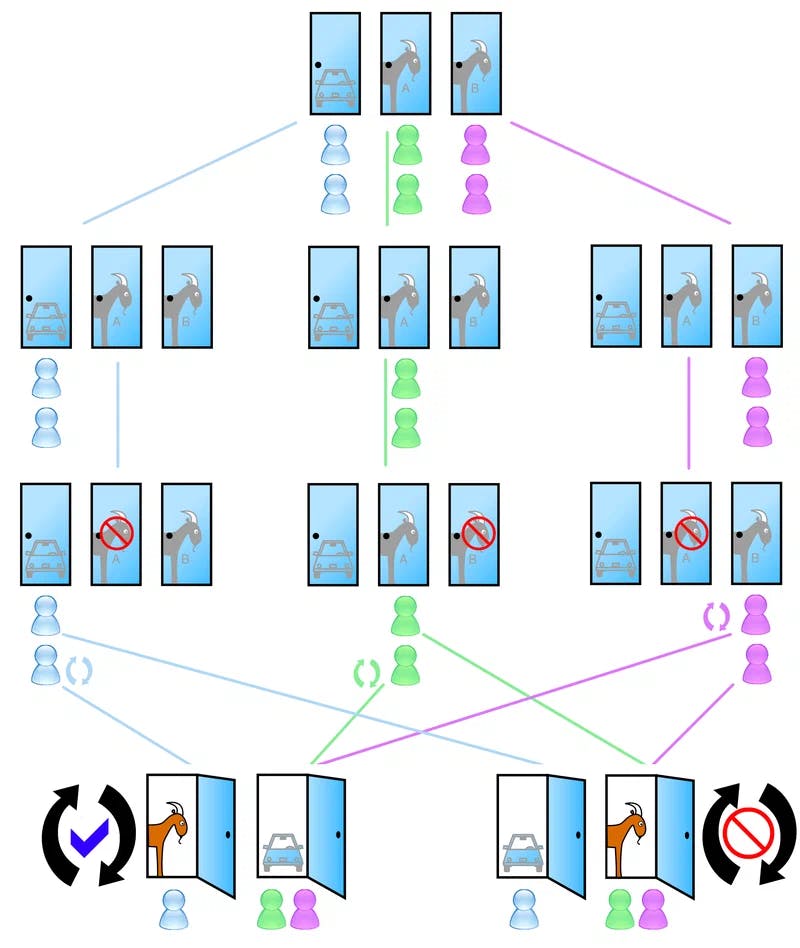
You are taking part in a TV show, where you can win a prize by guessing the door behind which the prize is hidden. You have three doors to choose from, and behind two of them showrunners put goats, so you need to choose. When you first choose a door, the host of the show will open another door from the one that you chose, and will show you a goat behind the opened door (surely there will be one). After that, he asks you if you want to change your initial decision, and pick another door from what you've already chosen. The question is: is it worth it to change your mind after a host shows you a goat, or there is no point in this change?

This is a paradox because at the first glance it seems like we don't have any reason to change our minds. The naive thoughts should look like this: if I pick the first door, and the host opens door number two, then I have an equal chance to get a prize if I choose door one or door three since the prize did not move.

The beautiful thing is that our intuition does not help us here, since, there is a point in changing a door! Let's look at some cases:

• If you initially picked a prize door, then after changing a decision you will fail. This happens in 1 case out of 3.

• If you initially picket a goat door, after changing a decision you will certainly win (since the host has shown the other door with a goat). This happens in 2 cases out of 3.

So, changing a door in this game leads to around 66% chance to win! This is much better than a 50/50 choice.

Wikipedia page also contains a beautiful visualization to understand it better, if you did not get it from my fuzzy explanation. Take a look:

Let's now look at a simple simulation code that can be useful to better understand this paradox:

The output examples show that we increase our chances to win if we change the door up to 2/3. This is a paradox because we tend to think it should not matter, but it actually is a crucial choice.

But the whole Monty-Hall story is just a starter, we are going to dive deep with the task that was suggested to me by my friend D.P.S. This task is also a famous one, but I never ever heard about it before. It's a task about prisoners and boxes.

Here's the task:

Consider 100 prisoners, each one has his own number (from 1 to 100). Someone took 100 pages and wrote down their numbers and after that put all these pages inside 100 boxes (all the same, each box contains one number, and numbers are inserted in boxes randomly). Each box also has its own number, but the numbers inside the box and on the box are independent. Then the prisoners were told that they should go one by one inside a room with these boxes and each one has to start opening the boxes until he finds his own number inside the box. Each one is allowed to open 50 boxes. No one knows what boxes were opened by another prisoner. If all of the prisoners will find their corresponding number, they will be free. Do the prisoners have a good chance to get freedom (is there an algorithm)?

When I first saw this task I did not come up with any good idea. We cannot choose a fixed set of boxes for all the prisoners to check, and if they choose randomly they will have very low chances to win since each one has a probability to find his own number equal to 1/2 if he randomly checks 50 boxes of 100. Since there are 100 prisoners with this strategy we will have a chance to win equal to (1/2)^100.

Try to think about this task for I while (I sure tried, but did not succeed) and then refer to this great explanation. It turns out to be a very neat yet effective strategy for the prisoners:

Let the prisoner has number i. He enters the room and checks the box with the number i on it. If his number is inside - he wins, if not he sees number j inside the box. Then he should check the box with the number j on it and repeat the logic. He will at most have 50 checks if he does not find his number - prisoners lose.

This is for sure a strategy that is not random, but why is it good? In fact, all these boxes and numbers are simply a permutation and the prisoners will lose only if there is a loop longer than 50 inside the permutation that the boxes represent. Chances for such an event are around 0.69, please refer here for more details.

So if we use the described strategy chances to win should be around 0.31, which is quite good. This may seem a bit more tricky than Monty-Holl paradox (although it has something in common), but let's look at an example code to check it:

I was just astonished by such a beautiful and simple solution. For me, these tasks have something in common and both describe that our intuitive way of thinking about choices is not efficient in the real world. If you've already seen such tasks or know some more please let me know in the comments.

That's all for today!

Feel free to comment, subscribe to my blog for more and have a great day!

Wish you to always make the right choices and never fall for paradoxes.