About half a year after I started my master's study in a new city (thus it was in 2015), I began attending special meetings that are called «career day», which were held in my university several times a year. These events were created as a platform for promising students and interesting employers from different companies (in IT and IT-related fields), where useful business connections could be created. Best of the best students and undergraduates could try their strength and get internships or even apply for full-time jobs after graduation. There are different opinions about such events, someone can think that this may interfere with good academic researches and prevent talented students to continue their path in science. In my opinion such «career day» meetings are very useful, because academia is definately not a dream for everyone, and even if you don't won't to find a job right away some connections never can be needless. Plus, you can always take away some notepads and T-shirts from such events, and nothing helps best to study math than new notepads =)
I started this story from «career day» for a good reason, since during one of such meeting I eventually got acquainted with a «wise-men and hats» family of tasks. These are very common logic puzzles and it is very possible that you've heard about at least one of the variation of these tasks. Today I will be talking about several interesting ones, that are also useful in terms of some algorithmic thinking (and even more, but no spoilers here). Here is the first one that I would like to discuss in this article:
Some king had a team of 100 wise-men counselors, and one day he got so terribly angry that he decided to test their wisdom. So he invited them in the evening into his palace and warned that tomorrow when the dawn breaks they will be put in one line in the garden near the palace, so that each one will be able to see only people ahead of him (i.e. the last one in line sees 99 people before, the first one sees nobody ahead). After that they will be blindfolded and one servant will put a hat on the head of each wiseman. Hats can be only black and white, and nobody knows which color will be put on him, and there is no limit in number of black and white hats. Then they will be allowed to look again, but only ahead (no turning heads), and the executioner will start asking each wiseman, starting from the last one in the line, what is the color of the hat he is wearing right now. Each one must call out his guess about color loudly when he is asked. Every man who answers correctly will be spared, but if wiseman will tell wrong color, he will be immediately executed in the garden. Then the king let wise-men go away in terror. They talked through this awful situation all night long, and after much thought thay have come to a smart algorithm how they could be answering so that at least 99 of them will survive (and maybe even 100, if they will be lucky enough). What algorithm did they come to?
Before we start solving this task, I propose you to think of it a bit by yourself, this is a very good mental exercise. In the meantime I will share how I picture these wise-men in my imagination (quite tough guys, I guess):

Ok, so now let's discuss. The first naive strategy that comes in mind is usually to call the color of the man that is directly ahead of you. So, if you are a wiseman in line and you see a white hat on a man that is next in line, your answer will also be «white». This way the man next to you will know his color and answer correctly and will survive. The next will repeat your approach, and so on. This is definately some strategy, but, unfortunately, a bad one, since in the worst case half of the wise-men will be executed in such a case (try to think of the worst-case example). Another strategy would be calling colors randomly, but this is even worse (in the worst case not a single wiseman will survive). What are we missing?
Well, the thing that we are missing is that every man sees all the line ahead. So the last man in line can see 99 people ahead, thus he already knows color of all the 99 people ahead of him (if only he does not have poor eyesight, which we suppose is not true =)). Now with that piece of information try to think once again on the task and come to a better strategy for wise-men before reading the next section where I give the correct answer.
Now let's think of the following strategy:
Think of a black hat as of number 1 and a white hat as of number 0. This way we can count sum of all hats ahead of each person, and we can know if this sum even or odd. If it is even than one can see even number of black hats ahead (because only even number of ones can result in even sum). Now we can correspond a color to the parity of colors that one can see ahead (i.e. take this sum modulo 2 and tell «white» if it results in 0 or «black» if results in 1). Suppose that the last wiseman in line (the one who can see 99 colors ahead) when he is asked for a color of hat he is wearing calls out the color corresponding to the parity of sum of 99 hat colors that he sees ahead. If he is lucky enough then this will correspond to the color that he is wearing and he will survive, if not he is executed (oops...). But now the second man in line can know two things: first, he heard what the previous wise man told («black» or «white») and second, he can see 98 hat colors ahead and count their parity. This way, if the parity that previous wiseman told and the parity that he can see with his eyes are the same, he is definately wearing a white hat (since «white» == 0), and if not, he is wearing a black one (since parity can change only by adding odd number, and the only possible odd corresponds to black color). The next one in line will have three pieces of information: the parity told by the first man who was asked for color, the parity called out by the next one asked and the parity of hats he sees ahead. Then he makes similar operation: he calculates color of his own hat by combining these three parities (i.e. by calculating sum modulo 2) and calling out corresponding color. This will continue until the first man in line (who can see nobody ahead) will have to only calculate sum of all parities that were called out and tell the corresponding color as a result.
So the main idea here is to work modulo 2 and calculate your color as a number corresponding to parities. That's quite a beautiful approach and allows 99 wise-men to survive anyway. I tried to visualize this approach for better understanding with this small picture (first row in this pic is the logic of answer of the last man in line, second row is a logic for some man in between first and last):
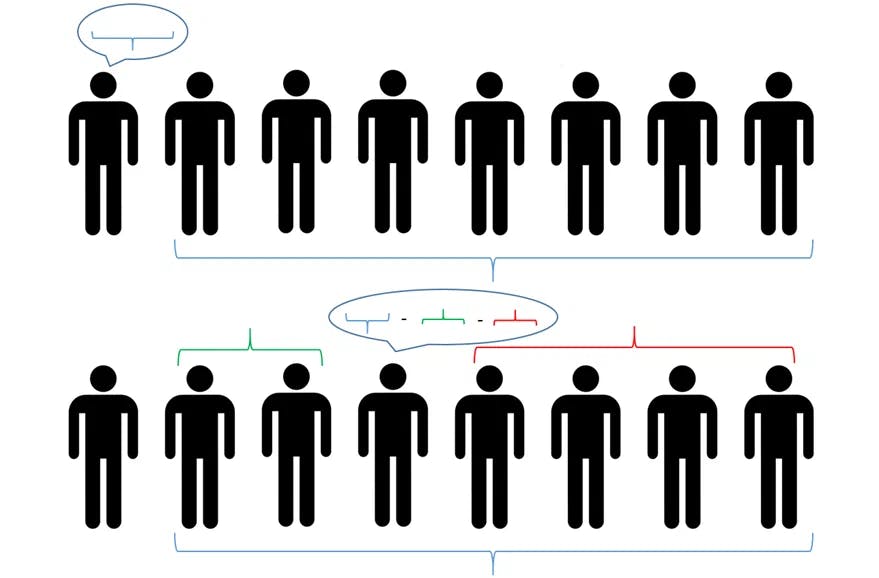
But if everything is so neat with modulo 2 logic, why can't we generalize this task for different modulo? I.e. if we suppose that there are not only 2 colors for hats, but m colors, and if we set number of wise-men from 100 to some variable amount n, we can recieve a very concise solution, which I've put in python code for better understanding. Take a look:
Now, from the mathematical point of view, the most important thing in this task is that wise-men are standing in one line and can see colors ahead and call out their colors loudly — these are the pieces of information that we can work with and make conclusions from. If we suppose different conditions where same wise-men are sitting at one table, and watch each others colors, but do not know the color of hat they are wearing, then we come to the classical form of the task, about which you can have a nice discussion with friends and relatives (or with some strangers, everyone deserves some beauty of formal logic). But even in such a variant of a task one can get to interesting constraints that make it fresh and new. One of such forms of a task I've heard from my wonderful colleague and brilliant mathematician Bistrigova Anastasiya. Here's what she sent me:
We took part in IPSC competition in 2018, it is a programming competition where ICPC-styled tasks appear (algorithmic tasks with jury-defined answers), as well as optimization tasks (where jury do not know the answer beforehand and competitors try to find the best one), game-tasks and even some comic tasks as well.
Among several tasks one appeared especially interesting for me, the one about hats, since it reminded me the things I did in my scientific work during my bachelor, master and even PhD studies - function decoding, i.e. repairing a function from some partial knowledge about it only using specific requests.
The task statement can be found here, but let's consider its main content briefly:
a) 13 wise-men agree on some strategy when each of them raises hand and when do not raise(this will be used for decision making),
b) When the game starts all of the wise-men close their eyes and someone puts a hat on each of the wiseman, hats can have one of two colors (let's call them red and blue),
c) After that all of them can open their eyes and see colors of everyone around except for the color on their own head. Using the strategy they discussed before the start of the game each wiseman decides whether he should or should not raise his hand,
d) Now each wiseman can see the result of decision of all the players around. Each one of them must now simultaneously tell the right color of the hat that they are wearing.
So the target is to develop such a strategy before the game begins that in any case each wiseman will be able to guess the color of his hat, using only information they see around.
The solution had to be implemented using language that we did not know (Lua 5.3), but the main difficulty was not in this constraint, of course. :-) The most difficult part was to find a good strategy for wise-men.
This task had a partial score and full score. Partial score was for the task when hats could be only of 2 colors, and full score if the number of colors is 4000.
Wow, that's what I call a good task, and the case of two colors looks very similar the the previous task that we could solve using parity information. Try to think of some solution yourself before reading further.
Ok, let's try the following strategy:
During the stage when everyone decides if he has to raise hand: each wiseman counts parity of sum of colors of hats that he can see(the idea is the same, let one hat be 1 and the other be 0), and raises hand only in case if this sum is odd (i.e. parity == 1).
During the stage when one should call his hat's color: wiseman number i selects any other wiseman with number j, calculates parity of sum of hats colors on all the wise-men he sees, except for number j (he definately sees all of them, just ignores number j). Then he compares this calculated parity to the signal from wiseman j based on the raised hand (if the hand is raised, we think signal is 1, otherwise it is 0). If the parity and signal are equal, then wiseman i has a hat with color corresponding to 0, otherwise to 1, and he can call it out.
This solution seem to be quite different if we compare it to the solution of the previous task, but some similar logic still can be found. The trick is that every wiseman sees equal amount of other people and thay have additional source of information: raised or not raised hands. The strategy that I described above can be visualized with the following scheme:
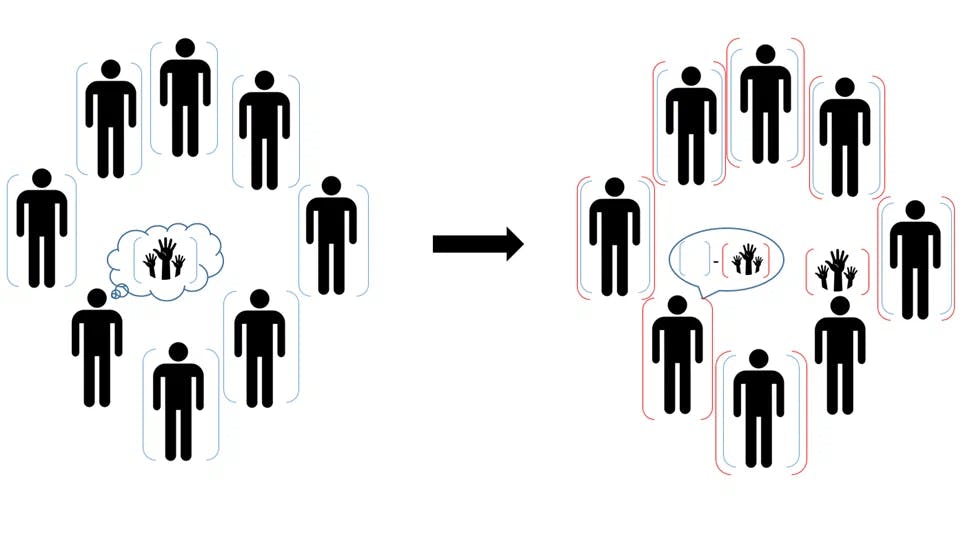
In this picture left side is the first stage of the process, where each wiseman decides if he wants to raise a hand (thus he calculates parity of hat colors), and on the right side is a process of guessing color of the hat (we find difference between «raised hand» parity and «color» parity).
If my description was not informative enough, please take a look at the following code (in which the case with only two colors is presented):
Ok, we already earned partial score, that's cool! But what should we do with the full-score case, how to solve the task if we have not 2, but 4000 colors? Here we cannot play with even-odd parity (number modulo 2), since our modulo is now larger, but can we use it instead? Well, the problem is that one raised hand is just one bit of information... But how did then authors of the task come up with number 4000? Now I propose you to stop and think a little before reading ahead, since it is a very good excercise for your computer-science intuition!
Ok, I bet you mentioned that 4000 is not just a random number, it is quite close to number 4096, which is (what a coincidence) a power of two (2^12 = 4096), and exponent is just one less than number of wise-men. These are all not just random pieces of information, we need to make a full picture now. To be fair, when I thought about this task for the first time I could not construct the full solution in detail, although the idea of bit-planes here was already clear. Here is the solution from Anastasiya herself:
For the 4000 colors case everything should be much trickier and it is very heartwarming that our team eventually did get the final solution. Partially I had inspiration from the theorem that I used in my scientific work, which is devoted to complexity of decoding a function of the following type: f(x_1, x_2, ..., x_n) = x_i xor x_j. For the curious ones this is a Proposition 6 from here, where the main idea is not to find i and j themselves, but to retrieve these numbers using their binary representation.
Let's note that we have 13 wise-men and 4000 colors, and 4000 < 2^12, thus it probably will be useful to consider binary representations of colors. 12 men could be somehow carrying information about the color of the hat, and 13th man could somehow hold total parity.
I hope that now when you get the basic idea, the full solution will be clear:
1) Wiseman with number j (j!=i) can see all the other people that wiseman i sees, except for j himself. He can calculate parity of (i-1)th bit in representation of sum of all the players he can see (excluding i). If parity that he calculated is the same as the parity of wiseman i, than (i-1)th bit in binary representation of j-th hat color is 0, otherwise it is 1.
Thus, wiseman 13 can calculate all the bits of his hat, wiseman 1 can compute all the bits except 0-th, wiseman 2 can calculate all the bits except 1-st and so on...
2) Using information from wiseman 13 everyone will be able to restore the missing bit. Consider wiseman 1, he sees every hat that wiseman 13 sees, except his own. He knows parity of sum of wise-men 2-12, also he knows parity of already calculated bits so far for his own hat's color. But wiseman 13 knows all this information + the missing bit of 1st wiseman. So if wiseman 1 somehow considers difference between parity that he calculated, and wiseman 13 calculated, he can know the 0-th bit in his hat color.
For the curious ones full solution can be found here, and author's solution contains one more strategy for the case of 2 colors.
Ok, if that is not beautiful, than what is? I did not manage to make the neat scheme for this explanation, but the idea should be clear from the description. Wise-men 1-12 will work on dedicated bit-planes and calculate parities only on them, and wiseman 13 will calculate parity of all the bits that he sees. Numbers in this task are not random, of course, we would not be able to do the same trick with 4100 colors, for example.
If still this is not clear enough, take a look at the following listing, where I tried to explain the logic via some example code:
Well, that was tricky. One more thing to mention before this article ends is that all the given constructions are heavily related to Error Correction Codes, which are so fantastically beautiful, that I beg you to look through them a bit in a spare time.
Thank you for reading, and thanks again to Anastasiya Bistrigova for a beautiful task as an idea for this article!
Wish you all the best, and never loose your head, or else how would you be wearing all these colorful hats?
